팩토리얼, 지수시간에 비해 빠르지만 입력 크기가 커질수록 처리 시간이 급격히 증가하는 알고리즘 범주에 속한다.
이 복잡도는 이중 반복문이 포함된 구조에서 자주 나타나며, 작은 입력에선 문제없지만, 큰 입력에서는 비효율적인 성능을 보인다.
대표적으로 정렬 알고리즘 중 버블 정렬, 삽입 정렬, 선택 정렬이 이에 해당하며, 브루트포스 방식의 문제 해결에서도 볼 수 있다.
버블 정렬
오름차순 기준
배열의 인접한 두 원소를 검사하고 정렬한다.

길이가 n인 배열이 있다.
전체 루프 i는 첫 번째부터 마지막 요소 앞 n-1까지 진행한다.
내부 루프 j는 인접한 두 요소를 비교하고 더 큰 수인 경우 교환을 진행하여 n - 1 - i까지 진행한다.
루프마다 가장 큰 요소가 순서대로 끝에 배치된다.
def bubble_sort(arr):
n = len(arr)
# 총 n-1회 반복
for i in range(n - 1):
# 정렬된 요소를 제외한 범위에서 반복
for j in range(n - 1 - i):
# 인접한 요소 비교 후 순서가 잘못되면 교환
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
data = [5, 2, 4, 3, 1]
print("정렬 전:", data)
bubble_sort(data)
print("정렬 후:", data)
"""
정렬 전: [5, 2, 4, 3, 1]
정렬 후: [1, 2, 3, 4, 5]
"""
모든 요소를 반복적으로 비교 및 교환한다. 어떤 경우든 i 반복은 무조건 n-1번을 수행하게 되며 이미 정렬된 배열인 경우에도 불필요한 반복이 진행되게 된다. 이러한 점을 개선해 스왑 발생 여부를 확인하여 정렬이 된 상태인 경우 조기 종료를 시킬 수 있다.
def bubble_sort_optimized(arr):
n = len(arr)
for i in range(n - 1):
swapped = False
for j in range(n - 1 - i):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
swapped = True
# 스왑이 한 번도 없으면 이미 정렬된 상태
if not swapped:
break
data = [1, 2, 3, 4, 5]
print("정렬 전:", data)
bubble_sort(data)
print("정렬 후:", data)
최악이나 평균의 경우에는 모든 요소를 끝까지 비교하고 교환해야 하므로 시간 복잡도는 O(n^2)이다. 그러나 이미 정렬된 배열인 최선의 경우에는 비교만 수행되고 스왑이 한 번도 발생하지 않기 때문에 조기에 종료되어, 최적화된 구현에서는 O(n)의 시간 복잡도를 가질 수 있다.
선택정렬
매 반복마다 가장 작은 값을 찾아 맨 앞과 교환하는 방식이다. 정렬된 부분과 미정렬 부분을 구분하고, 매 단계마다 최솟값을 선택한다. 교환 횟수는 최대 n-1회이지만 비교는 항상 일정하게 많이 발생하기 때문에 최선/최악 구분 없이 O(n^2)이다.

비교 방식이 데이터 정렬 여부와 무관하다.
def selection_sort(arr):
"""
선택 정렬 함수
현재 위치 이후의 요소 중 최솟값을 찾아 현재 위치와 교환
"""
n = len(arr)
for i in range(n - 1):
min_index = i # 현재 위치를 최솟값 인덱스로 가정
# i 이후 요소들 중에서 최솟값 인덱스 탐색
for j in range(i + 1, n):
if arr[j] < arr[min_index]:
min_index = j
# 현재 위치와 최솟값 위치를 교환
if min_index != i:
arr[i], arr[min_index] = arr[min_index], arr[i]
data = [5, 2, 4, 3, 1]
print("정렬 전:", data)
selection_sort(data)
print("정렬 후:", data)
"""
정렬 전: [5, 2, 4, 3, 1]
정렬 후: [1, 2, 3, 4, 5]
"""
구조가 단순하고, 교환 횟수가 적기 때문에 메모리 이동 비용이 큰 환경에 적합하지만 비교 횟수가 많고 입력이 정렬되어 있어도 시간 복잡도가 항상 O(n^2)인 단점이 있어 대규모 데이터에는 부적합하다.
삽입 정렬
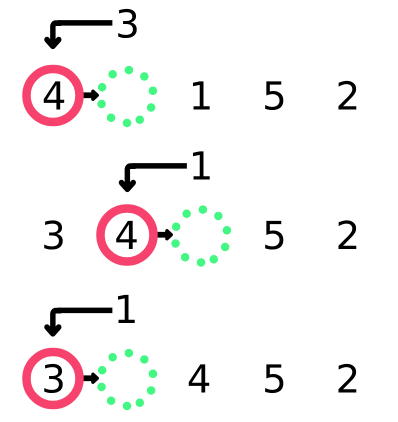
삽입 정렬은 배열의 두 번째 요소부터 시작하여, 현재 요소를 그 앞에 있는 요소들과 비교하면서 적절한 위치를 찾아 삽입하는 방식이다. 비교 과정에서는, 앞의 요소가 현재 요소보다 크면 한 칸씩 뒤로 이동시키고, 더 작은 값을 만나거나 배열의 처음까지 도달하면 그 자리에 현재 요소를 삽입한다. 이 과정을 반복하며 배열의 왼쪽 부분부터 정렬된 상태가 된다.
def insertion_sort(arr):
"""
삽입 정렬 함수
배열의 각 요소를 순차적으로 '정렬된 부분'에 삽입하여 정렬하는 알고리즘.
"""
n = len(arr)
# 두 번째 요소부터 시작: 첫 번째 요소는 이미 '정렬된 부분'으로 가정
for i in range(1, n):
key = arr[i] # 현재 정렬할 값
j = i - 1 # key 앞의 마지막 인덱스
# key가 정렬된 부분의 값보다 작으면, 한 칸씩 오른쪽으로 이동시켜 자리 비움
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
# 최종적으로 key를 알맞은 위치에 배치
arr[j + 1] = key
data = [5, 2, 4, 3, 1]
print("정렬 전:", data)
insertion_sort(data)
print("정렬 후:", data)
"""
정렬 전: [5, 2, 4, 3, 1]
정렬 후: [1, 2, 3, 4, 5]
"""
정렬된 배열일 경우 비교만 하고 이동이 거의 없어 O(n)에 가까운 성능을 보인다.
구현이 간단하며, 안정 정렬이기 때문에 동일한 값을 가진 요소들의 상대적 순서가 유지된다. 추가적인 배열 없이 입력 배열 내부에서만 정렬 수행을 하기 때문에 메모리에 효율적이지만 전체가 정렬되지 않은 경우 비교, 이동이 많아져 시간 복잡도는 O(n^2)가 된다.
'Coding > Algorithm' 카테고리의 다른 글
| O(2^n) - 지수 시간 (1) | 2025.07.12 |
|---|---|
| NP - TSP (1) | 2025.07.11 |
| P, NP (0) | 2025.07.08 |
| O(n!) - 팩토리얼 시간 (2) | 2025.07.08 |
| 빅-오(Big-O) 표기법 (1) | 2025.07.08 |